算法树
树表示由边连接的节点。我们将具体讨论二叉树或二叉搜索树。
二叉树是用于数据存储目的的特殊数据结构。二叉树具有特殊条件,即每个节点最多可以有两个子节点。二叉树具有有序数组和链表的优点,因为搜索与排序数组一样快,插入或删除操作与链表中一样快。
重要条款
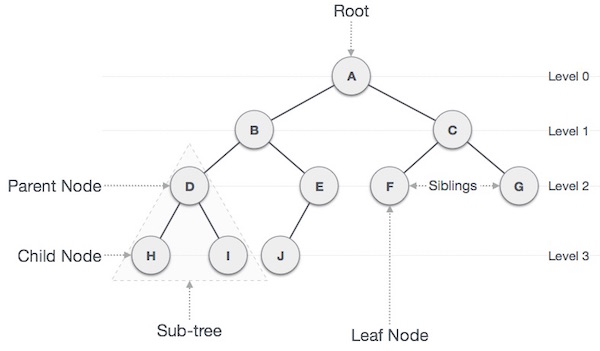
以下是关于树的重要术语。
路径 - 路径是指沿树边缘的节点序列。
Root - 树顶部的节点称为root。 每个树只有一个根,从根节点到任何节点只有一条路径。
Parent - 除根节点外的任何节点都有一条边向上到名为parent的节点。
Child - 由其边缘向下连接的给定节点下方的节点称为其子节点。
Leaf - 没有任何子节点的节点称为叶节点。
子树 - 子树表示节点的后代。
访问 - 访问是指在控制在节点上时检查节点的值。
遍历 - 遍历意味着以特定顺序遍历节点。
级别 - 节点级别表示节点的生成。 如果根节点处于级别0,则其下一个子节点处于级别1,其孙级处于级别2,依此类推。
keys - Key表示节点的值,基于该节点对节点执行搜索操作。
二进制搜索树表示
二叉搜索树表现出特殊的行为。节点的左子节点必须具有小于其父节点值的值,并且节点的右子节点必须具有大于其父值的值。
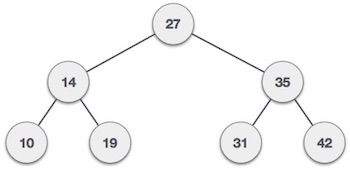
我们将使用节点对象实现树并通过引用连接它们。
树节点
编写树节点的代码与下面给出的类似。它有一个数据部分和对其左右子节点的引用。
struct node {
int data;
struct node *leftChild;
struct node *rightChild;
};
在树中,所有节点共享公共构造。
BST基本操作
可以在二叉搜索树数据结构上执行的基本操作如下 -
插入 - 在树中插入元素/创建树。
搜索 - 搜索树中的元素。
Preorder Traversal - 以 预订方式遍历 树。
Inorder遍历 - 以有序方式遍历树。
Postorder Traversal - 以后序方式遍历树。
我们将在本章中学习创建(插入)树结构并在树中搜索数据项。我们将在下一章中学习树遍历方法。
插入操作
第一次插入创建了树。之后,每当要插入元素时,首先找到其正确的位置。从根节点开始搜索,然后如果数据小于键值,则在左子树中搜索空位置并插入数据。否则,在右子树中搜索空位置并插入数据。
算法
If root is NULL
then create root node
return
If root exists then
compare the data with node.data
while until insertion position is located
If data is greater than node.data
goto right subtree
else
goto left subtree
endwhile
insert data
end If
履行
insert函数的实现应如下所示
void insert(int data) {
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
struct node *current;
struct node *parent;
tempNode->data = data;
tempNode->leftChild = NULL;
tempNode->rightChild = NULL;
//if tree is empty, create root node
if(root == NULL) {
root = tempNode;
} else {
current = root;
parent = NULL;
while(1) {
parent = current;
//go to left of the tree
if(data < parent->data) {
current = current->leftChild;
//insert to the left
if(current == NULL) {
parent->leftChild = tempNode;
return;
}
}
//go to right of the tree
else {
current = current->rightChild;
//insert to the right
if(current == NULL) {
parent->rightChild = tempNode;
return;
}
}
}
}
}
搜索操作
每当要搜索元素时,从根节点开始搜索,然后如果数据小于键值,则搜索左子树中的元素。否则,搜索右子树中的元素。对每个节点遵循相同的算法。
算法
If root.data is equal to search.data
return root
else
while data not found
If data is greater than node.data
goto right subtree
else
goto left subtree
If data found
return node
endwhile
return data not found
end if
此算法的实现应如下所示。
struct node* search(int data) {
struct node *current = root;
printf("Visiting elements: ");
while(current->data != data) {
if(current != NULL)
printf("%d ",current->data);
//go to left tree
if(current->data > data) {
current = current->leftChild;
}
//else go to right tree
else {
current = current->rightChild;
}
//not found
if(current == NULL) {
return NULL;
}
return current;
}
}