Shell排序算法
Shell排序是一种高效的排序算法,基于插入排序算法。该算法避免了大的移位,如插入排序的情况,如果较小的值是最右边的并且必须移动到最左边。
该算法对广泛传播的元素使用插入排序,首先对它们进行排序,然后对间距较小的元素进行排序。该间距称为 间隔 。此间隔基于Knuth的公式计算为 -
Knuth的公式
h = h * 3 + 1 where − h is interval with initial value 1
该算法对于中等大小的数据集非常有效,因为其平均和最差情况复杂度为0(n),其中 n 是项目数。
Shell排序如何工作?
让我们考虑以下示例来了解shell排序的工作原理。我们采用与前面示例中使用的相同的数组。对于我们的示例和易于理解,我们采用间隔4.创建位于4个位置的所有值的虚拟子列表。这些值是{35,14},{33,19},{42,27}和{10,44}
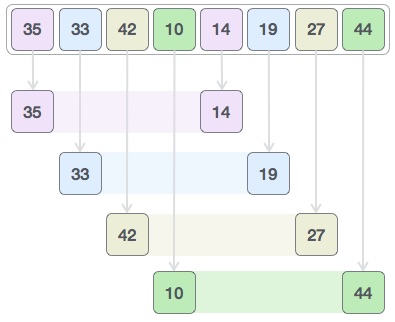
我们比较每个子列表中的值并在原始数组中交换它们(如果需要)。完成此步骤后,新数组应如下所示 -

然后,我们取1的间隔,这个间隙产生两个子列表 - {14,27,35,42},{19,10,33,44}
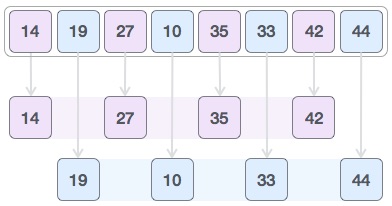
我们比较并交换原始数组中的值(如果需要)。完成此步骤后,数组应如下所示 -

最后,我们使用值间隔1对数组的其余部分进行排序.Thell sort使用插入排序对数组进行排序。
以下是逐步描述 -
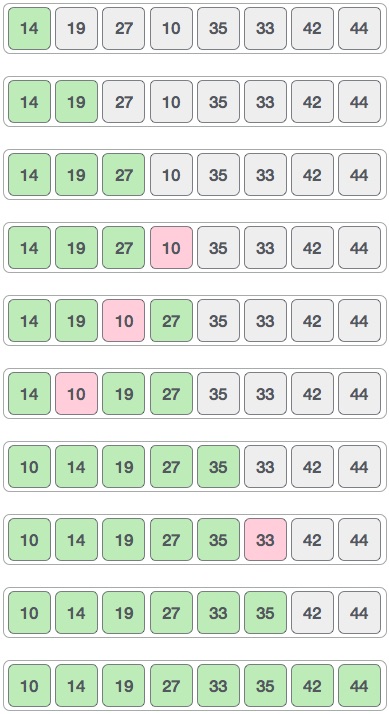
我们看到它只需要四次交换来对数组的其余部分进行排序。
算法
以下是shell排序的算法。
**Step 1** − Initialize the value of _h_ **Step 2** − Divide the list into smaller sub-list of equal interval _h_ **Step 3** − Sort these sub-lists using **insertion sort** **Step 3** − Repeat until complete list is sorted
伪代码
以下是shell排序的伪代码。
procedure shellSort()
A : array of items
/* calculate interval*/
while interval < A.length /3 do:
interval = interval * 3 + 1
end while
while interval > 0 do:
for outer = interval; outer < A.length; outer ++ do:
/* select value to be inserted */
valueToInsert = A[outer]
inner = outer;
/*shift element towards right*/
while inner > interval -1 && A[inner - interval] >= valueToInsert do:
A[inner] = A[inner - interval]
inner = inner - interval
end while
/* insert the number at hole position */
A[inner] = valueToInsert
end for
/* calculate interval*/
interval = (interval -1) /3;
end while
end procedure